Event-Diagnosis.

Diagnoser

Generator with state estimate attribute for event-diagnosis.

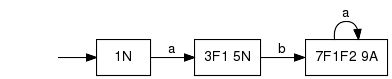
A diagnoser is a Generator with state attributes that provides state estimates for the diagnosed system G. While G models nominal and erroneous behaviour over the full alphabet Sigma, the diagnoser runs in parallel, but only synchronized w.r.t. the observable events Sigma0 ⊆ Sigma.

Each state estimate consists of a set of pairs (q,F). During diagnosis, the q components of the current diagnoser state indicate possible states in which the observed system G might be. The corresponding failure types f are those that occurred so far, provided that G indeed is in state q. In addition to the failures specified in the corresponding FailureTypeMap, f may be one of the predefined symbols N or A, to indicate nominal operation or ambiguity.

In this implementation, states of the original system are given by indices. Future versions may allow for optional symbolic state names to ease token identification.

Example:

The following figure shows a sample diagnoser with the alphabet Sigma={a, b} and the states Q={s1, s2, s3}.

Diagnoser automaton

In state s1 with label 1N, the original system is known to be in state 1 and no failure occred so far. In state s2 with label 3F1 5N, the original system either is in state 3 after a failure of type F1, or in state 5 without any failure so far. In state s3 with label 7F1F2, the original system either is in state 7 after failures of type F1 and type F2, or in state 9 with ambiguous failure history. The file output of the above diagnoser is depicted in the gray box. Here, the global attribute "FailureType" at the end of the token stream is the corresponding FailureTypeMap to define the semantics of each failure label.

<Generator>
"Diagnoser"   

<Alphabet>
"alpha"   "beta"   "gamma" 
</Alphabet>

<States>
%%% state s1
"s1"          
<StateEstimates>
1             
<DiagLabels> "N" </DiagLabels>
</StateEstimates>
%%% state s2
"s2"          
<StateEstimates>
3    <DiagLabels> "F1" </DiagLabels>
5    <DiagLabels> "N"  </DiagLabels>
</StateEstimates>
%%% state s3
"s3"          
<StateEstimates>
7    <DiagLabels> "F1" "F2"  </DiagLabels>
9    <DiagLabels> "A"  </DiagLabels>
</StateEstimates>
</States>

<TransRel>
"s1"          "a"           "s2"          
"s2"          "b"           "s3"          
"s3"          "a"           "s3"          
</TransRel>

<InitStates> "s1" </InitStates>
<MarkedStates></MarkedStates>

<FailureTypes>
%%% failure F1
"F1"   <FailureEvents> "WPblocked"   "WPfelldown"  </FailureEvents>
%%% failure F2
"F2"   <FailureEvents> "sfRunsContinuously" "cb1RunsContinuously" </FailureEvents>
</FailureTypes>

</Generator>

FailureTypeMap

Specification of Failure Types

The failure-type map defines failure-types f ∈ F that are each associated to a set Sigma_f of unobservable failure events. The sets Sigma_f of failure events are assumed to be disjoint, i.e. a failure-type map indeed defines a partition {Sigma_f| f ∈ F} of all failure events.

Optionally, each failure type f ∈ F may be equipped with a set of observable indicator events If ⊆ Sigma0. This feature is used for i-diagnosability, where a failure only needs to be detected after the occurence of a corresponding indicator event.

The example below defines one failure type F1 with failure- and indicator events.

<FailureTypes>
"F1"  
<FailureEvents>   "fail"    "error"  </FailureEvents>
<IndicatorEvents> "alpha"   "beta"    </IndicatorEvents>
</FailureTypes>