Omega Automata

This plug-in provides data types and functions to represent and operate on automata that process infinite-length words. For a general overview on the topic see [W1]. For the purpose of libFAUDES, we restrict the scope to support synthesis of supervisiors for non-termiating processes. For post- and pre-processing of omega automata with a varierty of expernal tools, libFAUDES exports to and imports from HOA formated files and streams; see [here] for further details.

Further details are organized as follows:


Copyright (C) 2010, 2025 Thomas Moor.

Omega Automata

Consider a genarator G and ignore the marking for now; we use the notation

G  =  (Q, Sigma, delta, Qo,  . )

with alphabet Sigma, state set Q, transition relation delta ⊆ Q x Sigma x Q, and initial states Qo. Assuming that G is free of deadlocks it can likewise model a non-terminating process. Denoting L(G) the generated star-language, we associate with G the generated omega-language

B(G)  :=  {v ∈ Sigma^w | all prefixes s < v are in L(G) }.

The crucial aspect from the infinite-length words perspective is the acceptance condition, a technical construct that after the elapse of all time decides whether or not a processed word w ∈ B(G) shall be considered an element of the accepted omega language. At this stage, libFAUDES addresses the Buechi acceptance condition and the Rabin acceptance condition.

Buechi Automata

A Buechi automaton technically matches the plain finite automaton; i.e., has the form G = (Q, Sigma, delta, Qo, Qm) with the marked states Qm. Specifically, we can use the faudes types Generator and/or System to encode a Buechi automaton.

With an infinite-length run pi on G we associate

  • w[pi] the corrosponding infinite-length word over Sigma, and

  • inf[pi] the set of states that have been visited infinitely often.

An infinite-length word v is accepted by the Buechi automaton G if there exists a corresponding run pi that visits at least one marked state infinitely often. The accepted omega-language associated with G is hence defined

Bm(G)  :=  {v ∈ Sigma^w | there ex. a run pi of G with v = w[pi] and inf[pi] ∩ Qm ≠ 0}

For deterministic generators, Bm(G) can be expressed as the limit of Lm(G):

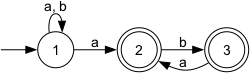
Bm(G)  =  B(Lm(G))  :=  {w ∈ Sigma^w | infinitely many prefixes s < v are in Lm(G) } .

In particular, for deterministic generators G1 and G2 with Lm(G1) = Lm(G2) we have Bm(G1) = Bm(G2).

Example

The automaton eventually-allways-alternate is defined over the alphabet Sigma={a, b}. It will generate an any sequence in Sigma^w and accept Sigma*(ab)^w.

G="eventually-allways-alternating"

Note that the above automaton is non-deterministic. It is the textbook example to demonstrate the restricted expressiveness of deterninistic Buechi automata: there exists no deterministic Buechi automate that accepts the same language.

Rabin Automata

A Rabin automaton is a tuple G = (Q, Sigma, delta, Qo, A), where the first entries are as for common automata and A is a set of pairs of state sets to encode a Rabin acceptance condition. Technically we have

A := { (Rp, Ip) | p ∈ P  | Rp, Ip ⊆ Q for p ∈ P }.

For an individual pair (Rp, Ip), p ∈ P, the set Rp shall be persistently recurrent and the set Ip shall be eventually invariant. An infinite-length run pi on G is accepted w.r.t. the pair (Rp, Ip) if it eventually stays within Ip and visits Rp infinitely often, i.e.,

inf[pi] ⊆ Ip and inf[pi]∩Rp ≠ 0 .

The run is accepted by the Rabin automaton if it is accepted by at least one pair (so called existential Rabin acceptance condition, not to be confused with universal Rabin acceptace). To this end, we have the associated omega-language

Rm(G)  :=  { v ∈ Sigma^w |
     there exists a run pi of G and p ∈ P s.t. v = w[pi], inf[pi] ⊆ Ip and inf[pi]∩Rp ≠ 0 }

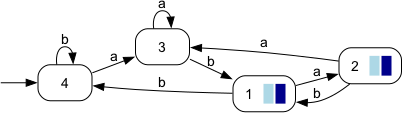
Example

The Rabin automaton variant of the eventually-allways-alternate example is again defined over Sigma={a, b} to accept Sigma*(ab)^w.

RA="eventually-allways-alternate"

Note that the above automaton is deterministic. It has been obbtained by the external tool ltl2dstar; see also the script safra.sh in the tutorial section of the omega-automata plug-in and how to ustilise external tools [here].

FAUDES type RabinAutomaton

The Omega-Automata Plug-In provides the faudes type RabinAutomaton. It is implemented along the line of the common Generator with additional data structures to encode the Rabin acceptance condition.

Token-IO example for a RabinAutomaton that accepts Sigma*(ab)^w. 

<Generator name="eventually-allways-alternate" ftype="RabinAutomaton">

<Alphabet> a b </Alphabet>
<States> 1 2 3 4 </States>
<TransRel>
1  a  2
1  b  4
2  a  3
2  b  1
3  a  3
3  b  1
4  a  3
4  b  4
</TransRel>
<InitStates> 4 </InitStates>
<MarkedStates/>

<RabinAcceptance>
<RabinPair> <R> 1 2 </R> <I> 1 2 </I> </RabinPair>
</RabinAcceptance>

</Generator>

Hanoi Omega-Automata Format (HOA)

The HOA format was introduced to facilitate the exchange of omega automata between different tools like ltl2dstar and Spot. It allows for a rather flexible specification of acceptance conditions, which for our purposes includes Buechi acceptance and Rabin acceptance.

To this end, we provide the executables gen2hoa and hoa2gen to convert libFAUDES formated generators to and from the HOA format. As an example, the above eventually-allways-alternate Rabin automaton will be converted to: 

~/libFAUDES/bin$ ./gen2hoa -s symtab.xml omg_dra.gen
HOA: v1
name: "eventually allways alternating a and b"
AP: 1 "ap0"
Alias: @a !0
Alias: @b 0
Start: 3
States: 4
acc-name: Rabin 1
Acceptance: 2 (Fin(0)&Inf(1))
--BODY--
State: 0 {1}
[@a] 1
[@b] 3
State: 1 {1}
[@a] 2
[@b] 0
State: 2 {0}
[@a] 2
[@b] 0
State: 3 {0}
[@a] 2
[@b] 3

In HOA, states are consecutively numbered starting from 0 and transition lables are logic formulas in terms of atomic propositions. For import and export, reindexing states is straight forward. Regarding libFAUDES events, they are first also encoded as consecutive integers starting at 0 and then theese integers are binary encoded as truth values of a sufficient number of atomic propositions. In the HOA output, the mapping is preserved by optional aliases. Since not all external tools maintaine aliases, gen2hoa can export a libFAUDES symbol table by the -s option. So after processing the exported HOA file, one can read back results and retrieve the original libFAUDES events.

In the above example, the HOA states 0 to 3 encode the libFAUDES states 1 to 4 and we have one atomic proposition ap0 with !ap0 representing the event a and ap0 representing event b. The symbol table amounts to 

<SymbolTable>
1    a
2    b
</SymbolTable>

where we again observe an offset of 1 since 0 is not a valid index in libFAUDES symbol tables.

For a complete example for exporting to HOA format, processing by an external tool and importing back the result, see safra.sh in the tutorial folder.

Literature

[W1] W. Thomas: Automata on infinite objects, Handbook of Theoretical Computer Science, 1990.

[W2] P.J. Ramadge: Some tractable supervisory control problems for discrete-event systems modeled by Buchi automata, IEEE Transactions on Automatic Control, vol 34, no 1, pp. 10-19, 1989.

[W3] R. Kumar, V. Garg, S.I. Marcus: On supervisory control of sequential behaviors, IEEE Transactions on Automatic Control, vol 37, no 12, pp. 1978-1985, 1992.

[W4a] J.G. Thistle, W.M. Wonham: Control of infinite behavior of finite automata., SIAM Journal on Control and Optimization, vol 32, no, 4, pp. 1075 - 1097, 1994.

[W4b] J.G. Thistle, W.M. Wonham: Supervision of Infinite Behavior of Discrete-Event Systems, SIAM Journal on Control and Optimization, vol 32, no, 4, pp. 1098 - 1113, 1994.

[W5] J.G. Thistle, H.M. Lamouchi: Effective Control Synthesis for Partially Observed Discrete-Event Systems, SIAM Journal on Control and Optimization, vol. 48, no. 3, pp. 1858 - 1887, 2009.

libFAUDES 2.33l --- 2025.09.16 --- with "omegaaut-synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-priorities-luabindings-hybrid-example-pybindings"

>>