| |
|
||||||
|
|
|||||||
|
Observer TestsThe observer plug-in supports the verification of properties of natural projections that are beneficial for the hierarchical supervisor synthesis. Here, two variants of the observer property are used for the nonblocking hierarchical control. Both conditions are verified for a given automaton G over the alphabet Sigma and a natural projection p0:Sigma*→Sigma0* with Sigma0 ⊆ Sigma. On the one hand, p0:Sigma*→Sigma0* is a natural observer for G if any string s ∈ L(G) can be extended to a string in Lm(G) whenever its projection p0(s) can be extended to a string in p0(Lm(G)).
Formally, p0 is a natural observer iff for all s ∈ L(G) and t ∈ Sigma0* On the other hand, p0 is a marked string accepting (msa) observer if it is a natural observer for the closed language L(G) and fulfills an additional condition for strings s ∈ L(G) that can be extended by an event o ∈ Sigma0 and such that the projection p0(s) is an element of p0(Lm(G)). For such strings, it must hold that there is a prefix s' ≤ s with the same projection, i.e., p0(s') = p0(s) and such that s' ∈ Lm(G). This condition ensures that whenever a string in the projected marked language p0(Lm(G)) is passed, each corresponding string in L(G) passes a marked string in Lm(G).
Formally, p0 is an msa-observer iff p0 is an L(G)-observer and for all strings s ∈ L(G) such that sSigma0∩L(G)! = 0 and p0(s) ∈ p0(Lm(G))
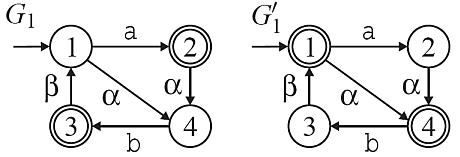
Here, p0 is a natural observer for G1 since it is possible to extend each string in L(G1) to a marked state by only following events in Sigma-Sigma0. However, p0 is not an msa-observer for G1 since for example the prefix epsilon of the marked string a can be extended by the event \alpha ∈ Sigma0 without passing a marked state. In contrast, p0 is an msa-observer but not a natural observer for G1'. The observer plug-in offers two additional functions for the verification of properties that allow the maximally permissive hierarchical supervisory control. Local control consistency ensures that a supervisor synthesis that is performed with an abstracted model yields the same result as a supervisor synthesis with the original model. The relevant components for this conditions are an automaton G, a natural projection p0:Sigma*→Sigma0* and an uncontrollable alphabet Sigma_uc. A natural projection p0 is locally control consistent w.r.t. a string s ∈ L(G), if for each uncontrollable event o_uc ∈ Sigma_uc∩Sigma0 that is feasible after the corresponding projected string, there is either no continuation or an uncontrollable continuation of s that terminates with o_uc. Hence, if o_uc is possible after s, then it cannot be prevented.
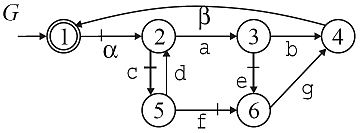
Formally, let G be an automaton over the alphabet Sigma, let Sigma_uc ⊆ Sigma be a set of uncontrollable events, and let Sigma0 ⊆ Sigma. The natural projection p0:Sigma*→Sigma0* is locally control consistent (lcc) w.r.t. a string s ∈ L(G) and Sigma_uc if for all o_uc ∈ Sigma0∩Sigma_uc s.t. p0(s)o_uc ∈ p0(L(G)), it holds that either there is no u ∈ (Sigma-Sigma0)* s.t. suo_uc ∈ L(G) or there is a u ∈ (Sigma_uc-Sigma0)* s.t. suo_uc ∈ L(G). Furthermore, we simply call p0 lcc if p0 is lcc for all s ∈ L(G). Local control consistency is illustrated by the automaton G and the projection to the alphabet Sigma0 = {\alpha,\beta} in the figure below. We consider all states (2,3,4,5,6) from which the uncontrollable event \beta ∈ Sigma0 can be generated after a local string in (Sigma-Sigma0)*. Noting that controllable events are marked by a tick, it is readily observed that there is a string with only uncontrollable events from any such state to the state 4, where \beta is feasible. Hence, local control consistency is fulfilled.
Finally, the mutual controllabilty condition is relevant for the combined hierarchical and modular supervisor synthesis of composed systems with multiple system components. It ensures that after any string of a composed system, the occurrence of an uncontrollable shared event is either feasible in all components that share it or it is infeasible in any component. Formally, the mutual controllability condition can be verified for component pairs:
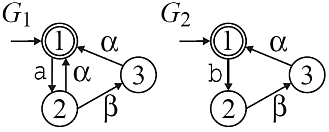
Let Gi,Gk be automata and define the projections p_i,k:(Sigma_i∪Sigma_k)*→Sigma_k* and p_k,i:(Sigma_k∪Sigma_i)*→Sigma_i*. Gi and Gk are mutually controllable if Mutual controllability is illustrated by the two automata G1 and G2 in the figure below, whereby it is assumed that the shared event \alpha is uncontrollable. Then, it is the case that although the event \alpha is possible in G2 after the occurrence of a, it is blocked due to the synchronization with H2 until \beta happens. Hence, mutual controllability is violated.
Regarding the implementation of the verification algorithms for the observer conditions and local control consistency, we exploit the fact that all conditions can be formulated in terms of a specific equivalence relation (quasi-congruence) on the states space of the automaton G [O5]. Hence the main task of our algorithms is to determine this specific equivalence relation for the respective conditions which can be done in polynomial time. The verification of mutual controllability requires a classical controllability test. IsNaturalObserverVerification of the natural observer property. Detailed description:For verifying if a natural projection has the natural observer property, a quotient automaton for GArg is constructed based on a specific equivalence relation (quasi-congruence) on the state space of GArg. If this quotient automaton is deterministic and only contains transitions with events in Sigma_h, the natural observer condition is fulfilled. IsMsaObserverVerification of the msa-observer property. Detailed description:For verifying if a natural projection has the msa-observer property, a quotient automaton for GArg is constructed based on a specific equivalence relation (quasi-congruence) on the state space of GArg. If this quotient automaton is deterministic and only contains transitions with events in Sigma_h, the natural observer condition is fulfilled. IsLocallyControlConsistentVerification of local control consistency (LCC). Signature:IsLocallyControlConsistent(+In+ System GArg, +In+ EventSet Sigma_h, +Out+ Boolean BRes) IsLocallyControlConsistent(+In+ Generator GArg, +In+ EventSet Sigma_c, +In+ EventSet Sigma_h, +Out+ Boolean BRes) Detailed description:For verifying if a natural projection fulfills the local control consistency condition, a backward reachability is conducted. If starting from a state, where an uncontrollable high-level event is feasible, at least one local state cannot be reached by an uncontrollable path, LCC is violated. IsOutputControlConsistentVerification of output control consistency (OCC). Signature:IsOutputControlConsistent(+In+ System GArg, +In+ EventSet Sigma_h, +Out+ Boolean BRes) IsOutputControlConsistent(+In+ Generator GArg, +In+ EventSet Sigma_c, +In+ EventSet Sigma_h, +Out+ Boolean BRes) Detailed description:For verifying if a natural projection satisfies the output control consistency condition, a backward reachability is conducted. If starting from a state, where an uncontrollable high-level event is feasible, a controllable event can be reached on a local backward path, OCC is violated. IsMutuallyControllableTest mutual controllability of two generators Detailed description:For verifying mutually controllability, two controllabilitys test for the given generators are performed. In each such test, one generator is considered as the plant, while the specification is computed by projecting the second generator to the alphabet of the first generator. If both controllability tests are successful, then mutual controllability is fulfilled. libFAUDES 2.33l --- 2025.09.16 --- with "omegaaut-synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-priorities-luabindings-hybrid-example-pybindings" |